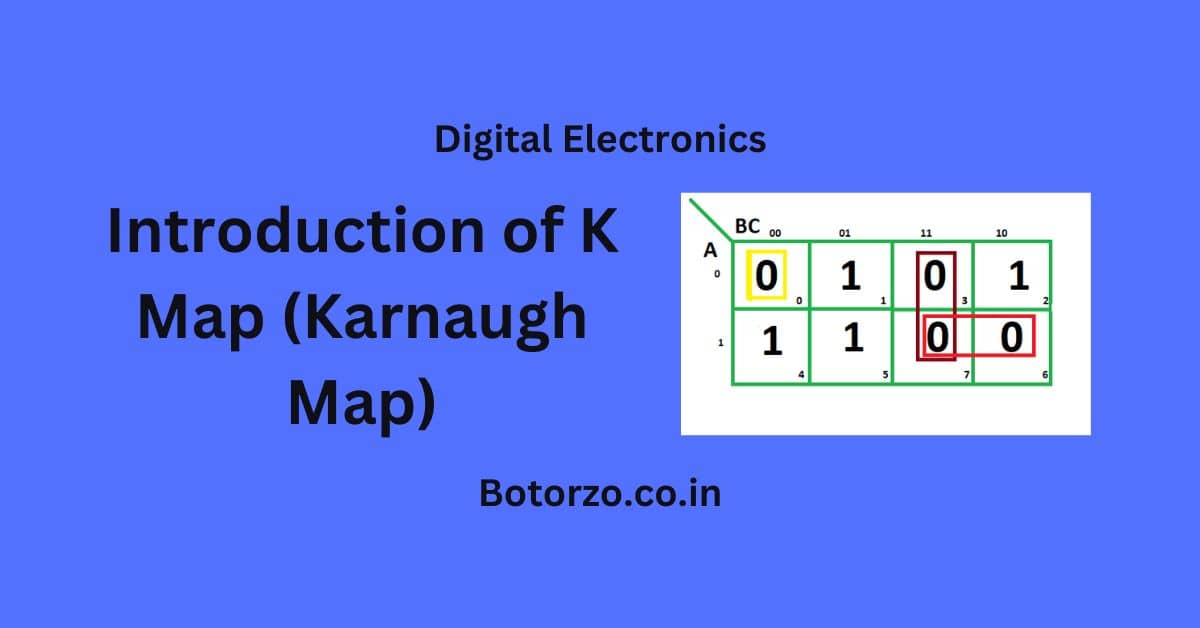
In this article, we will learn about the k map (karnaugh map), by using this tool any boolean expression can be minimized very easily.
The process of reducing a Boolean expression using boolean algebraic law methods in order to reduce the number of logic gates necessary to implement the expression is known as Boolean minimization. The goal is to create a circuit that is simpler and more efficient while performing the same logic function as the original expression.
The two most common approaches for performing Boolean minimization are algebraic operation and Karnaugh Map. The algebraic operation method simplifies the Boolean expression by employing Boolean laws and algebraic manipulation rules. A graphical representation of the Boolean expression is utilized in the K Map (Karnaugh Map) method to find groupings of nearby ones or zeros that can be joined to simplify the expression.
Boolean minimization produces a simplified expression with fewer variables and logic gates than the original expression. This can result in speedier, more efficient circuits with lower power consumption and costs. Boolean minimization is a critical stage in the design of digital circuits that are utilized in a wide range of applications such as computer processors, communication systems, and control systems.
What is Karnaugh Map?
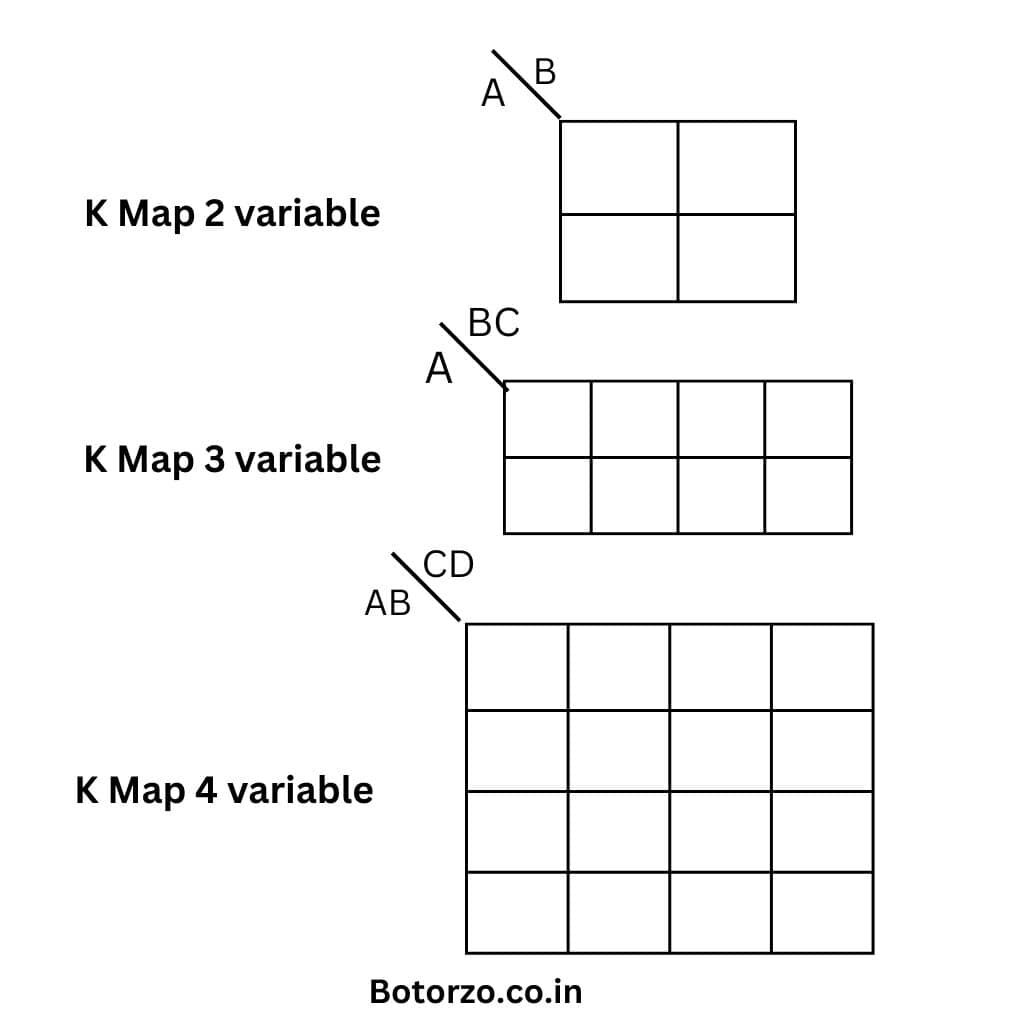
A K-map, or Karnaugh map, is a graphical way of simplifying Boolean expressions. It simplifies Boolean expressions with up to four variables in a methodical manner.
A K-map is a two-dimensional grid in which each cell reflects a distinct combination of inputs. Because the inputs are organized in a Gray code sequence, adjacent cells differ by just one variable.
It is used to find both minimized SOP and POS forms.
K maps can be used to identify problems in digital circuits in addition to simplifying Boolean expressions. When one of the input variables changes, the output briefly switches to an inaccurate value before settling on the proper value. K maps can be used to identify input combinations that may result in problems and to build circuits that remove or mitigate the effects of hazards.
What do K maps look Like?
Advantages And Uses Of K Map
Karnaugh maps (K-maps) are popular in digital circuit design for simplifying Boolean statements and reducing the number of logic gates necessary to build a circuit. Following are some specific applications , advantages and uses of K maps:
Boolean Expression Simplification:
K-maps give a graphical way for simplifying Boolean expressions with up to four variables. They can be used to find the largest groupings of adjacent ones or zeros, which can then be concatenated to construct a simpler Boolean statement. As a result, the circuit design is more efficient and compact.
Reduction of Logic Gates:
By employing K-maps to simplify Boolean statements, the number of logic gates necessary to construct the circuit can be lowered. As a result, the circuit is smaller, less expensive, and easier to build and test.
Hazard Identification:
In digital circuits, hazards can develop when a change in one input variable causes the output to briefly transition to an incorrect value before settling on the correct value. K-maps can be used to discover input combinations that may result in hazards and to build circuits that remove or mitigate the effects of hazards.
Digital Circuit Analysis:
K-maps can be used to examine digital circuits and verify their accuracy. They can be used to test circuit logic functions and confirm that the circuits match design criteria.
classroom to teach Boolean algebra
K-maps are also utilized in the classroom to teach Boolean algebra and digital circuit design. They give students with a visual and interactive tool for learning about digital circuits and Boolean algebra.
disadvantages of k map
Although Karnaugh maps (K-maps) are an effective tool for digital circuit design and analysis, there are a few disadvantages of k map to be aware of:
- Limitation to a Short Amount of Variables: K-maps can only simplify Boolean expressions with up to four variables. Other strategies, such as the Quine-McCluskey algorithm, may be better appropriate for formulations with more variables.
- K-maps are a manual technique that needs designers to manually identify and group cells. This can be time-consuming and error-prone, particularly for bigger K-maps.
- K maps may not be suited for increasingly complicated digital circuits with multiple inputs and outputs. Other methodologies, such as Boolean algebra or computer-aided design tools, may be more applicable in these instances.
- Can Provide Suboptimal Solutions: While K-maps can provide a simplified Boolean expression, they may not necessarily provide the best solution. Designers must use their discretion to assess whether the solution is appropriate for the given circuit design.
While K-maps have limits, they are nonetheless a useful tool in digital circuit design and analysis. Designers must evaluate their individual requirements and use K-maps in conjunction with other techniques to develop the finest possible digital circuits.