In this article, we will understand the concept of an open circuit. And like in the previous article on short circuits, we will understand the ideal case and the practical case of an open circuit.
Read About:- Short Circuit
Ideal Case Open Circuit
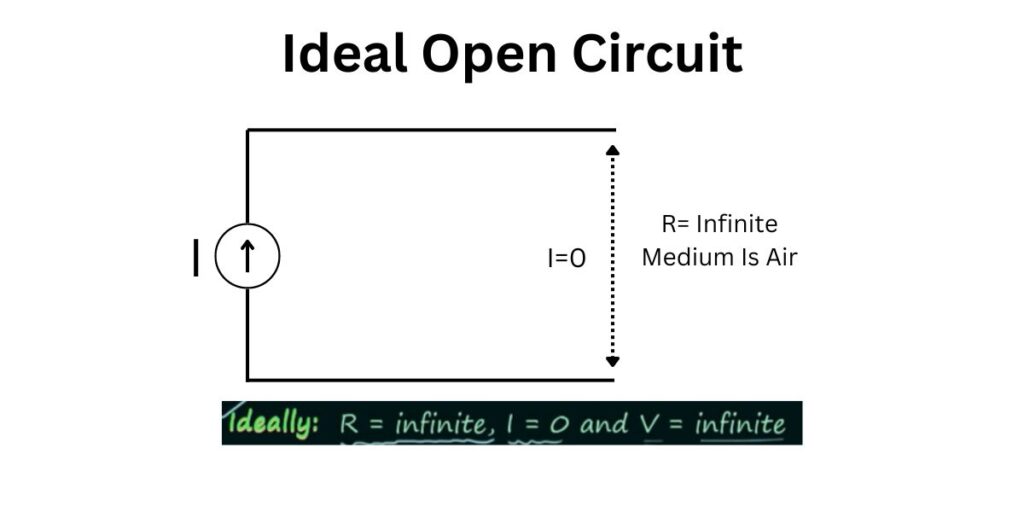
we will begin our discussion with the ideal case, Resistance of open circuit resistance of the path is infinite. This means you will have a path having infinite resistance, or you can see there will be no path. Like in this case, if See these two points with the dotted line, then you will find there is no path.
Air is having resistance, which is of very high value. So the air will act as the path which is having a resistance close to Infinity. And when this happens, it is very clear that the current will be equal to 0. if we talk about the voltage, then it is infinite. In the case of an ideal open circuit, it is infinite because resistance is infinite.
And if you calculate the drop, if you consider a very small current, very small current flowing through this path, you will find voltages going to be infinite. So ideally, the circuit should have the resistance of the path equal to infinite. The current flowing through the path will be zero amperes, and the voltage across the path is equal to infinite volts.
And here, in this case, we are violating KCL, KCL is violated in this case. And now we will understand how case KCL is violated. In this case, and how the violation of KCL implies the violation of the law of conservation of charge.
In this case, we are having a current source. And the current source is providing the current equal to I amperes. And I will enter the endpoint, And you can see that the current leaving or flowing from the dotted line is equal to 0 amperes, currentl I should be equal, which is not.
We know from the law of charge conservation that charges cannot be created or destroyed. But we’re destroying the charges here. So this particular case is not possible, practically, because here we are violating the case here. And this means we are violating the law of conservation of charge. And this is all for the ideal case of an open circuit.
Practical case Open Circuit
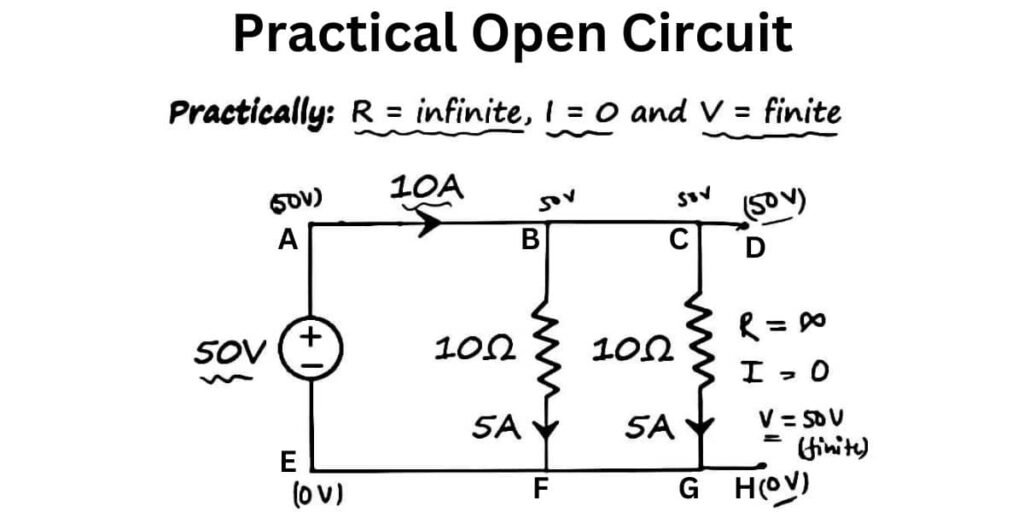
And now we will move on to the practical case. But before that, the circuit remains in the network, which is closed, like in this case, you can start a network is closed, but we are using the term open circuit. So how can a circuit be open when the circuit itself means closed network? So don’t confuse yourself.
This clearly means that we are having a path in the circuit which is having infinite resistance. Now let’s discuss the critical case of the open circuit. In this case, again, we are having the resistance equal to infinite ohms. Current equal to 0 amperes.
But the voltage is not infinite. It is the finite 50-volt source and the current it is providing is 10 amperes to the connection of two resistances as shown in the figure. And if we consider point D and point H, then you can see that we are having linear path. This means the resistance between these two points is equal to infinite.
And this means the current Through this path is equal to zero amperes. Now we will calculate the voltage across the path. We are having a voltage source equal to 50 volts. And if we consider points E, F, G, and H at 0-volt potential points A, B, C, and D will have a potential equal to 50 volts. Then in this scenario, you will get 50 – 0 equal to 50 volts as the voltage across DH.
So in the practical case of an open circuit, voltage is finite. This is all for the practical case of open circuit.